petit topic sur l 'angle que nous aimons tous
1. Equilibre d'une moto en virage
La moto est soumise à trois efforts : son poids, la force centrifuge, et la réaction de la route qui permet de compenser l'effet des deux efforts précédents : la composante verticale de la réaction s'oppose au poids, alors que la composante horizontale s'oppose à la force centrifuge.
La force centrifuge et le poids s'exercent au centre de gravité de l'ensemble moto+pilote, alors que la réaction de la route s'exerce au niveau de la zone de contact entre le pneu et le sol. Si l'on considère que cette zone de contact est ponctuelle et située dans le plan médian de la moto (à l'intersection du sol et de la ligne blanche tracée sur la photo du CBR ci-contre), on peut schématiser la situation de la manière suivante :
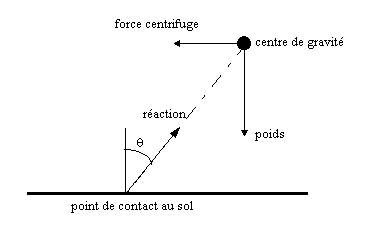
L'équilibre de la moto impose par exemple que le moment des efforts par rapport au point de contact au sol soit nul. Etant donné que la réaction s'exerce en ce point, les seuls efforts dont le moment ne sont pas nuls sont le poids et la force centrifuge. L'intensité du poids est P = m.g, où m est la masse de la moto et g la gravité. L'intensité de la force centrifuge est F = m.v2/r, où v est la vitesse et r le rayon de courbure du virage. Si l'on note h la hauteur du centre de gravité et q l'angle de la moto par rapport à la verticale, l'équilibre des moments s'écrit alors :
h.(cos q).m.v2/r = h.(sin q).m.g
La masse disparaît donc de l'équation, de même que la hauteur du centre de gravité, et il ne reste que
tan q = v2/(r.g)
Avec un tel modèle on montre donc que l'angle pris par une moto dans un virage ne dépend que du rayon de courbure de ce dernier et de la vitesse à laquelle on l'aborde.
2. Un modèle un peu plus réaliste
La situation se complique un peu si l'on prend en compte la forme du pneu.
La zone de contact au sol, que l'on suppose toujours ponctuelle, n'est en effet pas rigoureusement dans le plan médian de la moto, comme le montre le décalage angulaire qui existe entre les deux lignes tracées à partir du centre de gravité (approximatif) de la Yamaha d'OJ ... La situation une fois schématisée ressemble à ceci :
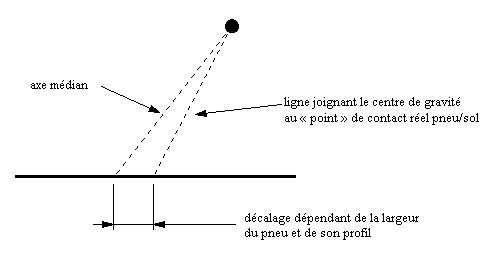
Si on zoome sur le pneu au niveau du sol, voici ce que l'on observe :
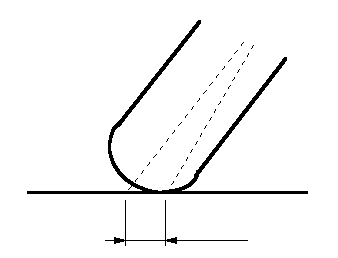
Notons d le décalage qui existe entre le point de contact réel et l'intersection sol/axe médian. Si on réécrit l'équilibre des moments (par rapport au point de contact réel), on obtient quelque chose du genre :
h.(cos q).m.v2/r = (h-d).(sin q).m.g
où q est toujours l'angle entre le plan médian et la verticale. On peut encore une fois simplifier par la masse, mais la hauteur du centre de gravité ne disparait plus :
h.v2/(r.g) = (h-d).(tan q)
ou encore
tan q = v2 / [r.g(1-d/h)]
Si la hauteur du centre de gravité augmente, d/h diminue (du moins pour un "d" donné), donc 1-d/h augmente ... donc tan q diminue : plus le centre de gravité est haut, moins il faut prendre d'angle.
Si le décalage d augmente (pneu plus large ou moins gonflé, par exemple...), on se retrouve dans la situation inverse : d/h augmente (pour h donné), donc 1-d/h diminue ... donc tan q augmente : plus on monte un pneu large, plus il faut prendre d'angle pour pouvoir passer un virage à une vitesse donnée.
On peut cependant relativiser l'influence de ces facteurs : en supposant que d soit de l'ordre de 70 mm et que h soit 10 fois supérieur, le coefficient "correcteur" 1-d/h est égal à 0.9. Cela signifie que pour un angle de 45° calculé avec le premier modèle, le fait de prendre en compte la largeur du pneu fait passer cet angle à 48° ...
je pense être complet
Accueil 
Dernières images 
S'enregistrer 
Connexion 
Mer 2 Avr 2008 - 10:56
intéressant!!! merci daniel! 
ça devient un forum d'intello 
appendice de substitution pour les nains en tréteau, permettant de compenser l'absence maladive d'équilibre... 
n'est plus usité, sauf par quelques autochtonees a proximité d'un lacet appelé xavée... 
ou ziiiiiiiiiiiiiip 
ou binnnnnnnnnng 
